Using regression variables

Introduction
Continuous regression variables
Categorical regression variables

Objectives: learn how to define and use regression variables (time varying covariates).

Projects: reg1_project, reg2_project

Introduction

A regression variable is a variable $x$ which is a given function of time, which is not defined in the model but which is used in the model. $x$ is only defined at some time points $t_1, t_2, \ldots, t_m$ (possibly different from the observation time points), but $x$ is a function of time that should be defined for any $t$ (if is used in an ODE for instance, or if a prediction is computed on a fine grid). Then, Mlxtran defines the function $x$ by intepolating the given values $(x_1, x_2, \ldots, x_m)$ . In the current version of Mlxtran, interpolation is performed by using the last given value:

$x(t) = x_j \quad \text{for} \ \ t_j \leq t < t_{j+1}$

Continuous regression variables

reg1_project (data = reg1_data.txt , model=reg1_model.txt)

We consider a basic PD model in this example, where some concentration values are used as a regression variable:

[LONGITUDINAL]
input = {Emax, EC50, Cc}
Cc = {use=regressor}
EQUATION:
E = Emax*Cc/(EC50 + Cc)

The predicted effect is therefore piecewise constant: it changes at the time points where concentration values are provided:

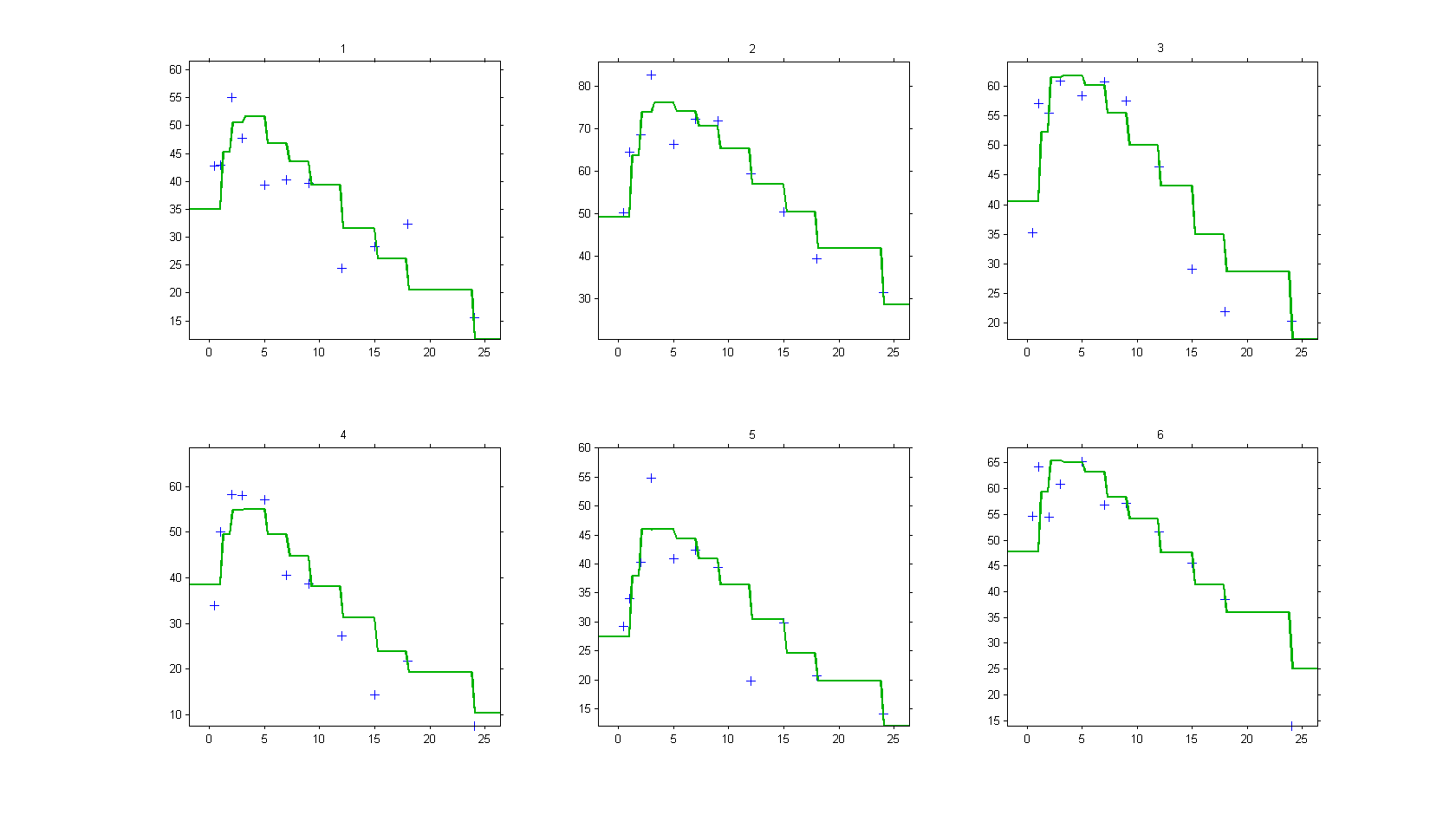
Categorical regression variables

reg2_project (data = reg2_data.txt , model=reg2_model.txt)

The variable $z_{ij}$ takes its values in {1, 2} in this example and represents the state of individual $i$ at time $t_{ij}$ . We then assume that the observed data $y_{ij}$ has a Poisson distribution with parameter $\lambda_1$ if $z_{ij}=1$ and parameter $\lambda_2$ if $z_{ij}=2$ . $z$ is known in this example: it is then defined as a regression variable in the model:

[LONGITUDINAL]
input = {lambda1, lambda2, z}
z = {use=regressor}
                           
EQUATION:
if z==0
   lambda=lambda1
else
   lambda=lambda2
end
DEFINITION:
y = {type=count, log(P(y=k)) = -lambda + k*log(lambda) - factln(k) }