Monolix includes a convergence assessment tool. It is possible to execute a workflow as defined above but for different, randomly generated, initial values of fixed effects. Click in the “Assessment” button to open the Assessment graphical interface.
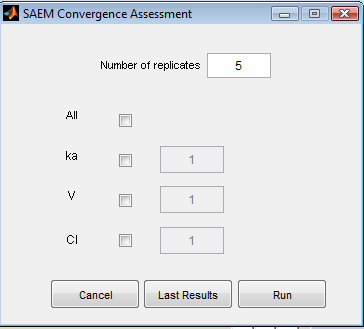
You can enter the number of runs, or replicates, the parameters to generate initial values and the intervals where those values should be (uniformly) simulated. Click on Run to execute the tool. Thus you are able to estimate the population parameters using several initial seeds and/or several initial conditions. Notice that you are able to set one initial parameter constant while generating the others. The minimum and maximum of the generated parameters can be modified by the user.
The workflow is the same between the runs and is the one defined in the interface (population parameters estimation must be selected). A result folder is generated for each set of initial parameters. Two kinds of graphics are given as a summary of the results
- one showing the estimated values (blue) with the estimated standard errors (red bars) for each replicate (if the Fisher information matrix estimation was included in the scenario)
- the superimposed convergence graphics for each parameter. In case of F.I.M estimation is included, then the black lines represents the mean of the estimated s.e..
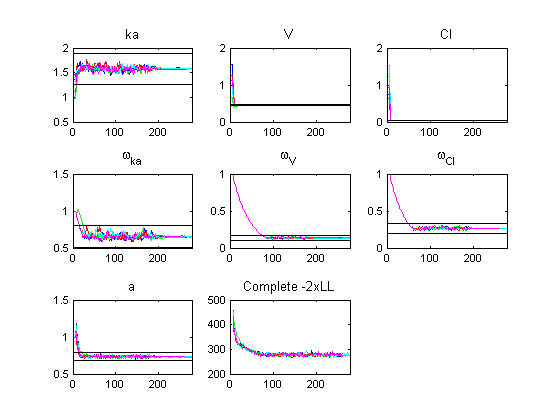
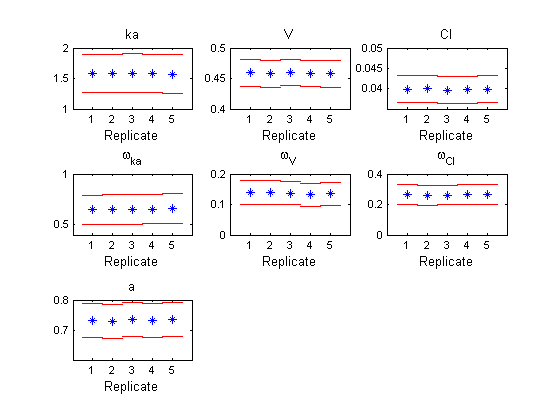
Also, a .mat file is produced with all the results used for those graphics. Press Last Results button to reproduce the last result graphics if you already have ran the tool for the current project, and Cancel to close the interface.
Best practices: what is the use the convergence assessment tool?
We cannot claim that SAEM always converges (i.e., with probability 1) to the global maximum of the likelihood. We can only say that it converges under quite general hypotheses to a maximum – global or perhaps local – of the likelihood. A large number of simulation studies have shown that SAEM converges with high probability to a “good” solution – it is hoped the global maximum – after a small number of iterations. The purpose of this tool is to evaluate the SAEM algorithm with initial conditions and see if the estimated parameters are the “global” minimum.
The trajectory of the outputs of SAEM depends on the sequence of random numbers used by the algorithm. This sequence is entirely determined by the “seed.” In this way, two runs of SAEM using the same seed will produce exactly the same results. If different seeds are used, the trajectories will be different but convergence occurs to the same solution under quite general hypotheses. However, if the trajectories converge to different solutions, that does not mean that any of these results are “false”. It just means that the model is case sensitive to the seed or to the initial conditions. The purpose of this tool is to evaluate the SAEM algorithm with several seeds to see the robustness of the convergence.