Select Page

Time-to-event data models

Objectives: learn how to implement a model for (repeated) time-to-event data with different censoring processes.

Projects: tte1_project, tte2_project, tte3_project, tte4_project, rtteWeibull_project, rtteWeibullCount_project

 

Introduction

Here, observations are the “times at which events occur”. An event may be one-off (e.g., death, hardware failure) or repeated (e.g., epileptic seizures, mechanical incidents, strikes). Several functions play key roles in time-to-event analysis: the survival, hazard and cumulative hazard functions. We are still working under a population approach here so these functions, detailed below, are thus individual functions, i.e., each subject has its own. As we are using parametric models, this means that these functions depend on individual parameters (\psi_i).

  • The survival function S(t, \psi_i) gives the probability that the event happens to individual i after time t>t_{\text{start}}:

    S(t,\psi_i) \ \ = \ \ \mathbb{P}(T_i>t;\psi_i) .

  • The hazard function h(t,\psi_i) is defined for individual i as the instantaneous rate of the event at time t, given that the event has not already occurred:

    h(t,\psi_i) \ \ = \ \ \lim_{dt\to 0} \frac{S(t,\psi_i) - S(t + dt,\psi_i)}{ S(t,\psi_i) \, dt} .

    This is equivalent to

    h(t,\psi_i) \ \ = \ \ -\frac{d}{dt} \log{S(t,\psi_i)} .

  • Another useful quantity is the cumulative hazard function H(a,b;\psi_i), defined for individual i as

H(a,b;\psi_i) \ \ = \ \ \int_a^b h(t,\psi_i) \, dt .

Note that S(t,\psi_i) \ \ = \ \ e^{-H(t_{\text{start}},t;\psi_i)}. Then, the hazard function h(t,\psi_i) characterizes the problem, because knowing it is the same as knowing the survival function S(t,\psi_i). The probability distribution of survival data is therefore completely defined by the hazard function.

Single event

To begin with, we will consider a one-off event. Depending on the application, the length of time to this event may be called the survival time (until death, for instance), failure time (until hardware fails), and so on. In general, we simply say “time-to-event”. The random variable representing the time-to-event for subject i is typically written Ti.

Single event exactly observed or right censored

  • tte1_project (data = tte1_data.txt , model=tte1_model.txt)

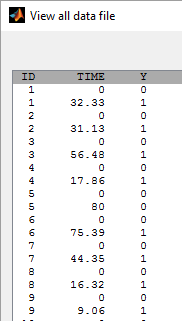
The event time may be exactly observed at time t_i, but if we assume that the trial ends at time t_{\text{stop}}, the event may happen after the end. This is “right censoring”. Here, Y=0 at time t means that the event happened after t and Y=1 means that the event happened at time t. The rows with t=0 are included to show the trial start time t_{\text{start}}=0:


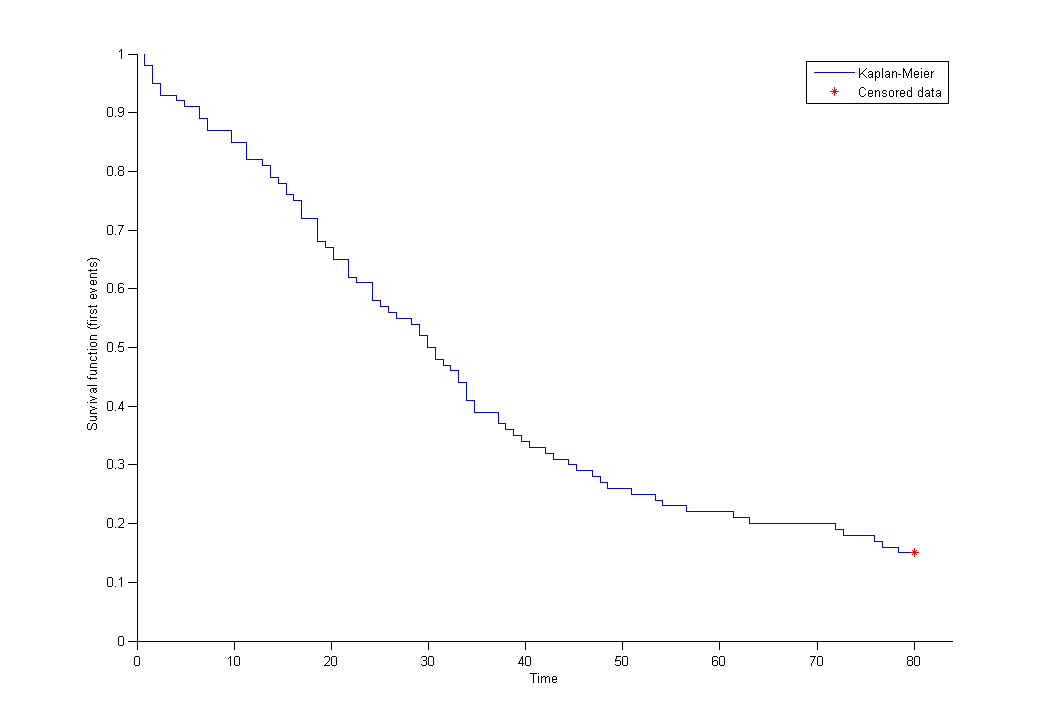
By clicking on the button plot the data, it is possible to display the Kaplan Meier plot (i.e. the empirical survival function) before fitting any model:

A very basic model with constant hazard is used for this data:

[LONGITUDINAL]
input = Te  
DEFINITION:
Event = { type = event,  hazard = 1/Te,  maxEventNumber = 1 }

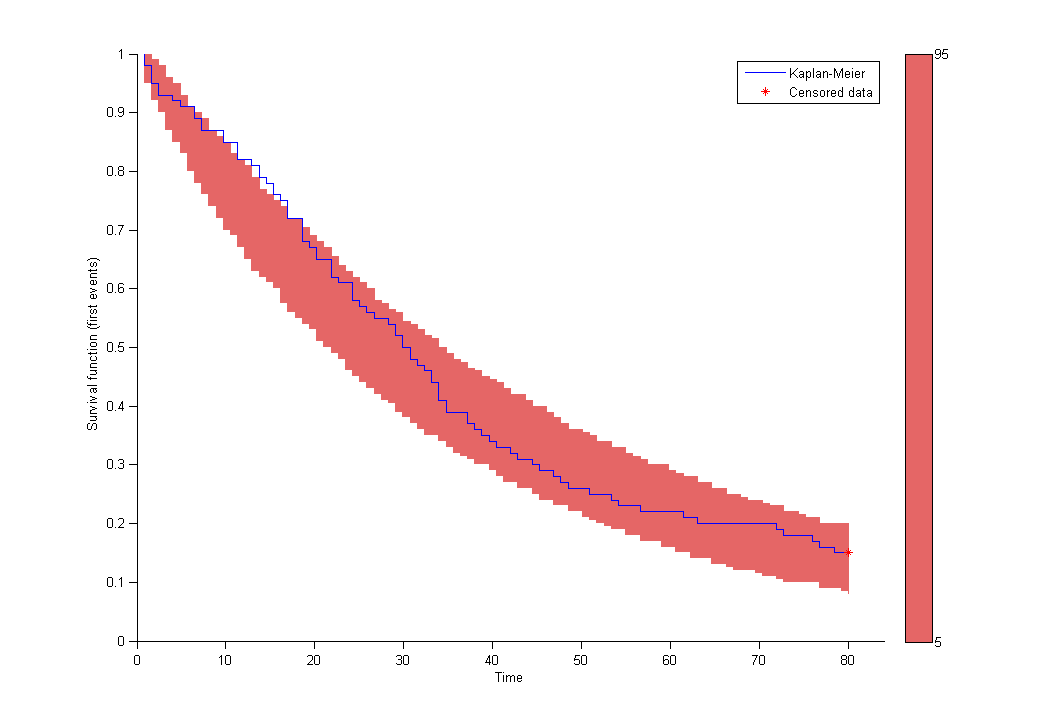
Here, Te is the expected time to event. Specification of the maximum number of events is required both for the estimation procedure and for the diagnostic plots based on simulation, such as the predicted interval for the Kaplan Meier plot which is obtained by Monte Carlo:

Single event interval censored or right censored

  • tte2_project (data = tte2_data.txt , model=tte2_model.txt)

We may know the event has happened in an interval I_i but not know the exact time t_i. This is interval censoring. Here, Y=0 at time t means that the event happened after t and Y=1 means that the event happened before time t.


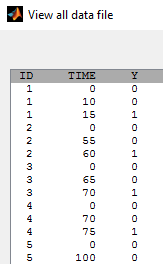
Event for individual 1 happened between t=10 and t=15. No event was observed until the end of the experiment (t=100) for individual 5. We use the same basic model, but we need now to specify that the events are interval censored:

[LONGITUDINAL]
input = Te  
DEFINITION:
Event = {type=event, 
         hazard=1/Te,
         eventType=intervalCensored, 
         maxEventNumber=1,
         intervalLength=5,       ; used for the graphics (not mandatory)
         rightCensoringTime=200  ; used for the graphics (not mandatory)
}

Repeated events

Sometimes, an event can potentially happen again and again, e.g., epileptic seizures, heart attacks. For any given hazard function h, the survival function S for individual i now represents the survival since the previous event at t_{i,j-1}, given here in terms of the cumulative hazard from t_{i,j-1} to t_{i,j}:

\begin{array}{ccl}S(t_{i,j} | t_{i,j-1};\psi_i) &=& \mathbb{P}(T_{i,j} > t_{i,j}\,|\,T_{i,j-1} = t_{i,j-1};\psi_i)\\&=&\exp(-H(t_{i,j-1},t_{i,j};\psi_i)) \\ &=&\exp(-\int_{t_{i,j-1}}^{t_{i,j}}h(t,\psi_i) dt) \end{array}

Repeated events exactly observed or right censored

  • tte3_project (data = tte3_data.txt , model=tte3_model.txt)

A sequence of n_i event times is precisely observed before t_{\text{stop}}=200:

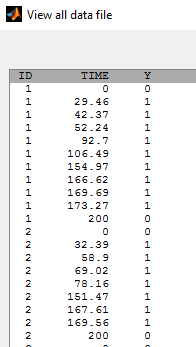
We can then display the Kaplan Meier plot for the first event and the mean number of events per individual:


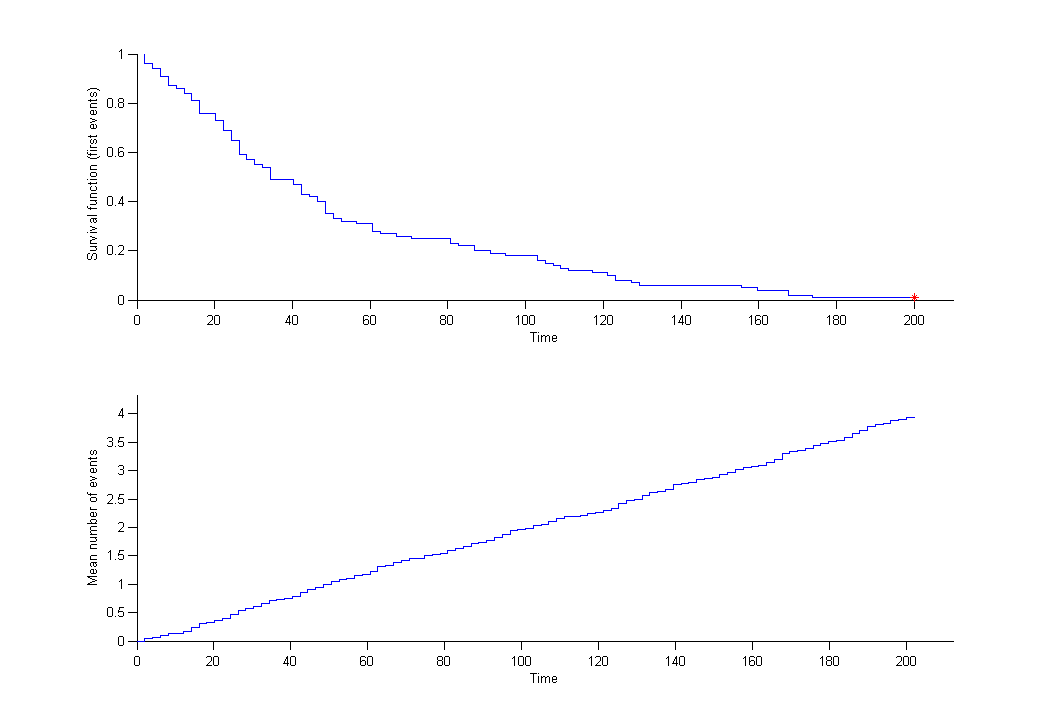
After fitting the model, prediction intervals for these two curves can also be displayed on the same graph.

Repeated events interval censored or right censored

  • tte4_project (data = tte4_data.txt , model=tte4_model.txt)

We do not know the exact event times, but the number of events that occurred for each individual in each interval of time:

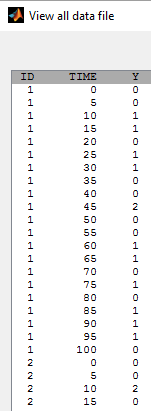
User defined likelihood function for time-to-event data

  • rtteWeibull_project (data = rtte_data.txt , model=rtteWeibull_model.txt)

A Weibull model is used in this example:

EQUATION:
h = (beta/lambda)*(t/lambda)^(beta-1)
DEFINITION:
Event = {type=event,  hazard=h}
  • rtteWeibullCount_project (data = rtteCount_data.txt , model=rtteWeibullCount_model.txt)

Instead of defining the data as events, it is possible to consider the data as count data: indeed, we count the number of events per interval. An additional column with the start of the interval is added in the data file and defined as a regression variable:


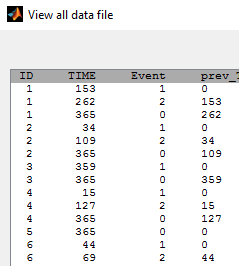
We then use a model for count data (see rtteWeibullCount_model.txt).

modal close image